Volver a la página de retos

SOLUCIÓN RETO 1: El valor de las flores

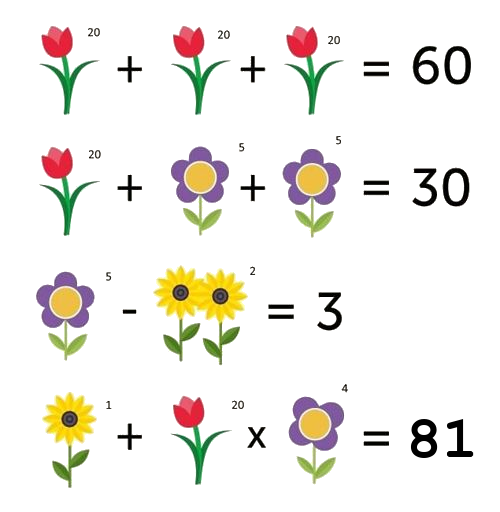SOLUCIÓN RETO 2: Hileras de flores

Si en el esquema del pasatiempo se desplaza la rosa que está en la fila central a la izquierda, hacia la derecha, se deshace una hilera, pero se generan dos, luego habrá una hilera de más, nueve en total. Y si se hace un movimiento similar con la rosa de la derecha, pero desplazándola hacia la izquierda, habrá diez hileras en total, como se muestra en la figura 1.

Figura 1		Figura 2

Otra posible solución para conseguir nueve hileras se muestra en la figura 2.

SOLUCIÓN RETO 3: Sujiko

SOLUCIÓN RETO 4: KenKen

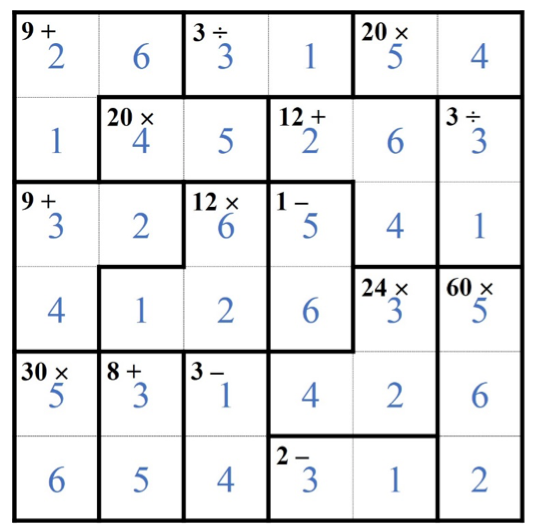SOLUCIÓN RETO 5: Número misterioso

Si el número inicial termina en 2, al multiplicarlo por 2, la última cifra del número final es 4; al colocar esta cifra en penúltima posición del número inicial y multiplicando por dos, resulta que la penúltima cifra del número final es 8; repitiendo este proceso de colocar cada cifra del número final en su posición del número inicial y multiplicar por dos hasta que nos quede la cifra 1 en el número inicial y la cifra 2 en el número final, llegamos a la solución 105263157894736842.

SOLUCIÓN RETO 6: Divisiones curiosas de una rosquilla y un pastel

SOLUCIÓN RETO 7: Bingo apilado

SOLUCIÓN RETO 8: Con todas las cifras

Algunas de las soluciones a este pasatiempo son:

123 – 45 – 67 + 89,

123 + 45 – 67 + 8 – 9,

123 + 4 – 5 + 67 – 89,

123 – 4 – 5 – 6 – 7 + 8 – 9,

12 + 3 – 4 + 5 + 67 + 8 + 9,

12 + 3 + 4 + 5 – 6 – 7 + 89,

12 – 3 – 4 + 5 – 6 + 7 + 89,

1 + 23 – 4 + 56 + 7 + 8 + 9,

1 + 23 – 4 + 5 + 6 + 78 – 9,

1 + 2 + 34 – 5 + 67 – 8 + 9,

– 1 + 2 – 3 + 4 + 5 + 6 + 78 + 9,

9 + 8 + 76 + 5 – 4 + 3 + 2 + 1,

98 – 7 – 6 + 5 + 4 + 3 + 2 + 1,

98 + 7 – 6 + 5 – 4 + 3 – 2 – 1.

SOLUCIÓN RETO 9: Las ocho reinas

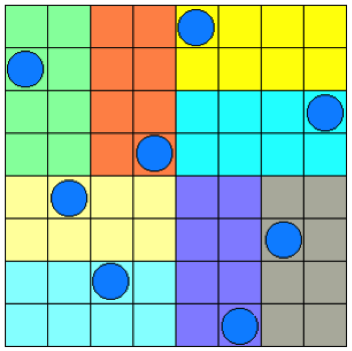SOLUCIÓN RETO 10: Cuestión de Creatividad

SOLUCIÓN RETO 11: Vigilancia

SOLUCIÓN RETO 12: Número Oculto

SOLUCIÓN RETO 13: Viajar en pareja

Como se trata de seis jugadoras que viajan en parejas, sólo puede haber tres medios de transporte. Como Sara y Patricia van juntas y no van en coche ni en avión, estos dos medios de transporte serán los utilizados por las otras cuatro jugadoras.

Como Laura viaja en avión y Eli no va en avión, Eli va en coche y no acompaña a Laura. Así que Eli debe acompañar a Ana o a Desiré.

Ahora bien, como Eli no va con Ana, Eli debe acompañar a Desiré y ambas irán en coche.

Por tanto, la respuesta es que Desiré va en coche.

SOLUCIÓN RETO 14: Partidas de ajedrez

Para resolver un problema lógico como este, así como cualquier juego de ingenio o problema matemático, hay que seguir cuatro pasos fundamentales:

1. antes de hacer, tratar de entender;
2. buscar estrategias para resolver el juego;
3. llevar adelante la estrategia elegida (y si te equivocas volver a empezar);
4. sacar jugo al juego y a la experiencia.

Como cada partida involucra a dos jugadores, entonces será la mitad de la suma del número total de partidas jugadas por A, B y C (les voy a llamar por las iniciales). Como (2+3+5)/2=5, se juegan 5 partidas.
Si Carmen jugó 5 partidas es que jugó en todas y nunca perdió, por lo que ganó la primera partida. Por tanto, las partidas fueron C-B, C-A, C-B, C-A y C-B.
Razonando de manera similar, la última partida la juegan Abel y Belén, pues si hay 9 partidas y Carmen sólo juega 4, como no puede estar dos seguidas sin jugar, necesariamente juega alternas la 2ª, 4ª, 6ª y 8ª.

SOLUCIÓN RETO 15: Con las pilas guardadas

Tras pensarlo un poco probablemente te parezca que hacen falta 8 intentos para hacer funcionar el juguete, el reto es conseguirlo con solo 7 intentos.

Si enumeramos las pilas del 1 al 8 y probamos las siguientes combinaciones de pilas:

12, 13, 23, 45, 56, 46, 78,

el juguete funcionará con alguna de ellas.

En efecto, si tras los tres primeros intentos el juguete no funciona, es porque entre las pilas 1,2,3 hay al menos 2 descargadas. De igual forma, si tras los intentos 6 primeros intentos el juguete no funciona, eso significa que además entre las pilas 4,5,6 hay al menos 2 descargadas. Si realizados 6 intentos el juguete no ha arrancado, eso significa que todas las pilas descargadas están numeradas con un número del 1 al 6. Por tanto, al probar la 7 y la 8 el juguete funcionará.

SOLUCIÓN RETO 16: A toda carrera

Ponemos a correr los 25 en grupos de cinco lo que nos da un total de 5 carreras con las que determinaremos los 5 más rápidos de cada grupo. Además, los dos últimos de cada carrera ya no pueden ser ninguno de los tres más rápidos.

Realizamos una segunda ronda con una carrera entre los cinco ganadores. El ganador será el más rápido de los 25, pero ninguno de los grupos pertenecientes al cuatro y cinco clasificados puede estar entre los tres más rápidos. Si reordenamos los cinco grupos iniciales según la clasificación de la segunda ronda, tenemos esta disposición, según el orden de llegada de la primera ronda:

Grupo 1: 1-2-3-4-5

Grupo 2: 6-7-8-9-10

Grupo 3: 11-12-13-14-15

Grupo 4: 16-17-18-19-20

Grupo 5: 21-22-23-24-25

Los únicos que pueden estar entre los tres más veloces, aparte del número 1, son el 2, 3, 6, 7 y 11. El resto ya tienen tres que son más rápidos que ellos.

La última ronda se efectúa con una carrera entre estos para determinar el segundo y tercero más veloces.

En total habremos necesitado 7 carreras.

SOLUCIÓN RETO 17: Aquí hay gato encerrado

Seis días. Si se abren las cajas en el siguiente orden 2, 3, 4, 4, 3, 2 se atrapará al gato, como mucho, en seis días. Que esa táctica funciona se ve en la siguiente tabla, en la que cada columna representando una caja y cada fila representando un día, y en la que el color de cada casilla indica: en verde las cajas en las que puede estar el gato cada día, en negro en las cajas que no puede estar, en marrón las cajas que se abren cada día y en rojo la caja en la que se le encontraría, de no haberlo hecho antes. Además, en 5 días no se puede conseguir. ¿Qué ocurre si el primer día abres la caja 3? ¿Y si es la caja 1?

También valdría el orden: 2, 3, 4, 2, 3, 4. De hecho, si el gato comenzó en una caja numerada con un número par lo encontrarás en uno de los 3 primeros días con la secuencia 2, 3, 4. Sin embargo, si comenzó en una caja con número impar, tras tres días estará en una con número par y repitiendo la secuencia 2, 3, 4. También lo atraparás en este caso.

SOLUCIÓN RETO 18: Triángulos y más triángulos

Es imposible hacerlo con menos de siete triángulos. Parece que la solución original es del gran divulgador de las matemáticas Martin Gardner y requiere unir un punto del interior del triángulo con cinco puntos, incluido el vértice del ángulo obtuso de modo que se formen cinco triángulos acutángulos.

SOLUCIÓN RETO 19: La edad de la lógica

El número del billete buscado es 27927 y la edad de la hija, 27 años.

Si la edad de la hija es ab, entonces el número del billete es abcab. Como la suma de las cinco cifras también da la edad de la hija, entonces a + b + c + a + b = 10 a + b. Es decir, b = 8 a – c. Si se toman valores de c desde 0 hasta 9 se obtienen los números de billetes (y edades) siguientes: 18018 (18), 17117 (17), 16216 (16), 15315 (15), 14414 (14), 13513 (13), 12612 (12), 11711 (11), 29729 (29), 10810 (10), 28828 (28) y 27927 (27). Por lo tanto, de todas las edades posibles: 10, 11, 12, 13, 14, 15, 16, 17, 18, 27, 28 y 29, la que cumple la condición “es la primera vez que ha podido volver a ocurrir después de unos cuantos años en que eso era imposible” es 27. Luego el número de billete es 27927.

SOLUCIÓN RETO 20: Rompecabezas triangular

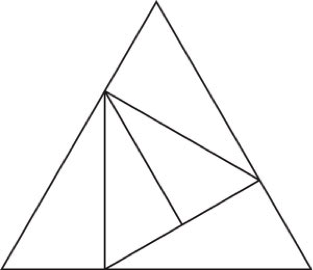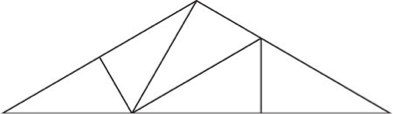Volver a la página de retos